While many students of pure and applied mathematics advanced them first hypotheses, she has been Benoit Mandelbrot to say first of all what had in common their theories, unendole inseme in an only new disciplina.Nato to Warsaw in 1924 and the spostatosi ones in endured France in 1935 from he tried to visualize the problems, or of attaccarli in geometric terms, when possible. It attended the ecole politechnique, then Caltech where it had to that to make for before the time with the chaotic movements of a fluid turbulento.Nel 1958 arrived to IBM, where it began a mathematical anlisi of the electronic noise and began to intravvedere a structure in it, a hierarchy of fluctuations of every dimension that could not have been explained from the existing statistical methods in those periodo.Attraverso the years that followed, problems that seemed between scollegati they were added in the crescent body of ideas that would have been called geometry frattale.Grazie to the computers that acquired always greater graphical abilities, the eye of its mind was supported from the visualization on monitor of frattali.Ancora once the models based on the frattali produced - than the experts they said to be similar the real phenomenon very. The visualization was extended also to the world fisico.In a provocative entitled article " How much is long the coast of Great Britain? " Mandelbrot noticed chela answer depends on the scale to which one measure: it always grows more as keeps account of every bay and insenatura, every sand stone, every granello. It discovered moreover " to the autosomiglianza " of many frattali - the reappearance of aspects geometrically similar to every scale. Mandelbrot has been name " IBM Fellow " in 1974 and from then it continues to work to IBM Watson Research Center.
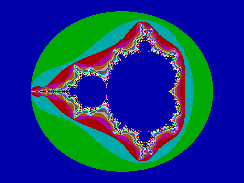
E' more the classic: it is the only frattale to being implemented in almost every program that generates them; from others come very many of the images of frattali recently pubblicate.Come many here also this are simply a diagram in which axis x he is real and the axis y is imaginary: every point in the plan characterizes a complex number. Hour a any point in the complex plan is taken to a any complex number - - and it calls C=(cx, cy), one constant. If ne it takes an other, than this time it can vary, and Z=(nx is called, ny). Leaving from Z=0 is estimated the Z^2+C value, takes the result, the checks to Z and it is estimated of new Z^2+C; the calculation is repeated many times: in terms mathematicians it comes iterata the function Z(n+1) = Z(n)+C. For some values of C, the result it stretches to zero after little. For other values it grows without limite.Il blue color refers to first, while the others depend on the iterance in which Z^2 it has exceeded value 4.
Here one simple procedure C that implements the frattale of Mandelbrot
void Mandel(void) {
int x, y, i; float nx, ny, cx, cy, oldx, sum; nx=0;ny=0;
for(x=-450, i=0;x < 190;x++) / / to use one resolution of
640x480 for(y=0, i=0;y < 240;y++) {
i=0;oldx=0;cx=(float)x/200;cy=(float)y/150;nx=0;ny=0; I give { i=i+1;
oldx=nx; nx=nx*nx-ny*ny+cx; / / { quadratic transformation }
ny=(2*ny*oldx+cy); / / { Zý+c } somma=nx*nx+ny*ny; } while(((sum)
< 4) && (< the 40)); / / { not to increase too
much to the iterances otherwise it puts us days!! } if (i==40) { i=0;
putpixel(x+450, y+240, 0); putpixel(x+450, -y+240, 0); } else{
putpixel(x+450, y+240, % 15); putpixel(x+450, -y+240, % 15); } }
while(!kbhit()); }
The formula of Newton is a used algorithm in order to find the roots of a polinomiale equation for successive attempts that converge to the correct value when the approximate value of new is introduced in the formula. It works very well, less than it is not therefore ill-fated to exactly take a value on the line between 2 roots. In this case the sequence explodes in the chaos with result that diverge hand more and more wildly by hand that the iterances are continued. The used polinomiale equation in the figure is Z^3-1=0, that it has the solutions in the complex plan, poichè Z is one variable complex.
This frattale has been gained magnifying a lot the frattale of Mandelbrot in around of the point in the complex plan C=(-0,8256;0,19465)
For knowing better than what to trattaVedere Sciences n.279 November 1991 p.118